컴퓨터 음수 표현 원리컴퓨터는 우리가 일상에서 사용하는 십진수 체계와 달리 이진수를 기반으로 모든 데이터를 처리한다. 특히 음수를 표현하는 방식은 컴퓨터 구조와 연산 효율에 직접적인 영향을 미치는 핵심 개념이다. 이 글에서는 컴퓨터가 음수를 표현하는 원리를 중심으로 보수 개념, 이진수 구조, 그리고 실제 연산에서 왜 2의 보수가 표준으로 사용되는지까지 체계적으로 설명한다.
보수 개념으로 이해하는 컴퓨터 음수 표현
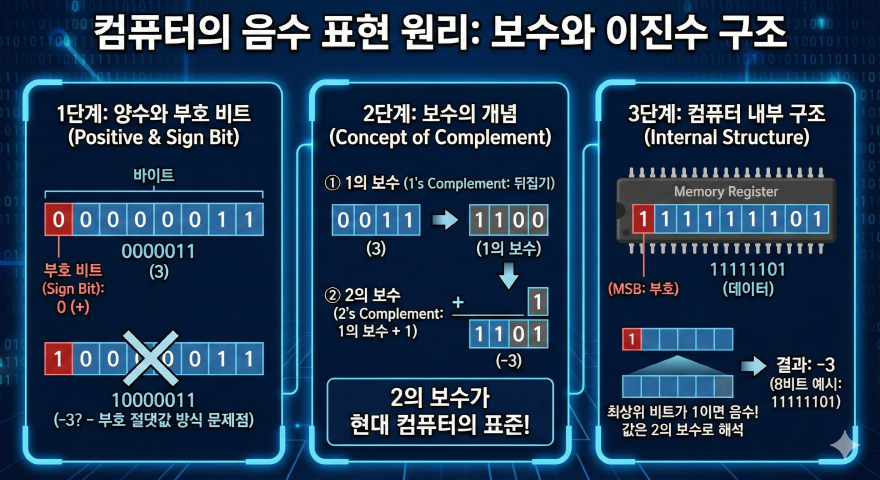
컴퓨터에서 음수를 표현하기 위해 가장 먼저 이해해야 할 개념은 보수이다. 보수란 특정 기준값에 도달하기 위해 필요한 수를 의미하며, 진법에 따라 정의가 달라진다. 십진수에서는 9의 보수와 10의 보수가 존재하고, 이진수에서는 1의 보수와 2의 보수가 사용된다. 컴퓨터는 감산 연산을 직접 수행하기보다는 덧셈 구조를 활용하기 때문에, 보수를 이용해 음수를 표현하고 계산한다. 이진수에서 1의 보수는 각 비트를 반전시키는 방식이다. 예를 들어 4비트 환경에서 0101의 1의 보수는 1010이 된다. 이 방식은 직관적이지만, +0과 -0이 동시에 존재하는 문제를 갖는다. 이러한 구조적 비효율성 때문에 실제 컴퓨터 시스템에서는 거의 사용되지 않는다. 반면 2의 보수는 1의 보수에 1을 더한 방식이다. 같은 예시에서 0101의 2의 보수는 1011이 된다. 2의 보수 체계에서는 0이 하나만 존재하며, 덧셈 회로 하나로 양수와 음수를 모두 처리할 수 있다.
이진수 기반 음수 표현 구조
컴퓨터는 모든 데이터를 비트 단위로 저장하며, 음수 역시 동일한 비트 구조 안에서 표현된다. 일반적으로 가장 왼쪽 비트는 부호 비트로 사용된다. 0이면 양수, 1이면 음수를 의미한다. 예를 들어 8비트 시스템에서 00000101은 십진수 5를 의미한다. 이 값의 2의 보수를 취하면 11111011이 되며, 이는 -5를 의미한다. 음수라는 개념은 인간의 해석일 뿐, 컴퓨터는 이진 패턴과 연산 규칙만을 따른다. 이진수 기반 음수 표현의 장점은 범위 설정이 명확하다는 점이며, 이는 CPU 설계와 연산 최적화에 직접적인 이점을 제공한다.
컴퓨터 구조에서 2의 보수가 표준인 이유
현대 컴퓨터 구조에서 2의 보수가 표준으로 자리 잡은 이유는 연산 회로 단순화, 0의 단일 표현, 비교 연산 효율성 때문이다. 덧셈기 하나만으로 모든 산술 연산을 처리할 수 있으며, 이는 성능과 전력 효율 향상으로 이어진다. 또한 대부분의 프로그래밍 언어와 CPU 아키텍처가 2의 보수를 기반으로 설계되어 있어 실무 활용성도 매우 높다.
컴퓨터의 음수 표현은 보수 개념과 이진수 구조, 하드웨어 설계가 결합된 결과물이다. 특히 2의 보수 방식은 연산 효율과 구조적 안정성 덕분에 현대 컴퓨터의 표준으로 자리 잡았다. 이 원리를 이해하면 컴퓨터 구조와 프로그래밍 전반에 대한 이해도가 크게 향상된다.