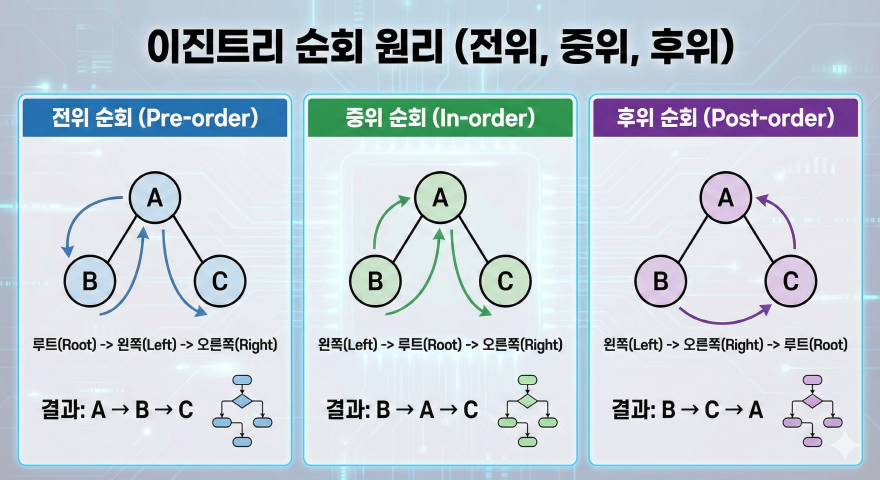
트리 자료구조에서 순회는 모든 노드를 한 번씩 방문하는 가장 기본적인 연산이다. 특히 이진트리에서는 전위(preorder), 중위(inorder), 후위(postorder) 순회 방식이 핵심 개념으로 사용된다. 이 세 가지 순회 방식은 방문 순서의 차이에 따라 전혀 다른 결과를 만들어내며, 알고리즘 문제 해결과 실제 시스템 설계 모두에서 중요한 역할을 한다. 이 글에서는 트리 운행법의 원리를 중심으로 각 순회 방식의 개념과 차이를 2026년 기준 최신 학습 흐름에 맞춰 정리한다.
전위 순회(preorder)의 구조와 개념
전위 순회는 루트 → 왼쪽 서브트리 → 오른쪽 서브트리 순서로 노드를 방문하는 방식이다. 이름 그대로 루트를 가장 먼저 방문하기 때문에 트리의 전체 구조를 빠르게 파악하는 데 유리하다. 전위 순회는 트리를 복사하거나 직렬화할 때 자주 사용되며, 계층 구조를 그대로 출력해야 하는 상황에서 효과적이다. 예를 들어 파일 시스템이나 조직도와 같이 상위 개념이 먼저 나타나야 하는 구조에서는 전위 순회가 직관적인 결과를 제공한다. 또한 전위 순회는 재귀 호출 구조와 매우 잘 어울리기 때문에 구현이 비교적 단순하다. 루트에서 시작해 왼쪽과 오른쪽으로 내려가며 동일한 규칙을 반복하기만 하면 된다. 코딩 테스트에서는 전위 순회를 통해 트리 생성 과정을 역으로 추론하는 문제가 자주 출제되며, 이때 루트 노드를 빠르게 파악할 수 있다는 장점이 있다. 이러한 특징 덕분에 전위 순회는 트리 구조를 이해하는 첫 단계로 많이 활용된다.
중위 순회(inorder)의 원리와 활용
중위 순회는 왼쪽 서브트리 → 루트 → 오른쪽 서브트리 순서로 노드를 방문한다. 이 순회 방식은 이진 탐색 트리(Binary Search Tree)에서 특히 중요한 의미를 가진다. 이진 탐색 트리를 중위 순회하면 노드 값이 오름차순으로 정렬된 결과를 얻을 수 있기 때문이다. 이 특성은 데이터 정렬, 검색 알고리즘, 범위 조회 등 다양한 실무 로직에서 활용된다. 중위 순회는 트리 내부의 상대적인 크기 관계를 자연스럽게 표현해주기 때문에 구조적 이해에도 도움을 준다. 학습 관점에서는 왼쪽, 현재, 오른쪽이라는 흐름이 다소 헷갈릴 수 있지만, 트리의 대칭 구조를 기준으로 생각하면 이해가 쉬워진다. 또한 중위 순회는 수식 트리에서 연산자의 우선순위를 자연스럽게 표현하는 데에도 사용된다. 이러한 이유로 중위 순회는 자료구조와 알고리즘을 깊이 있게 학습하는 과정에서 반드시 숙지해야 할 핵심 개념이다.
후위 순회(postorder)의 특징과 사용 사례
후위 순회는 왼쪽 서브트리 → 오른쪽 서브트리 → 루트 순서로 노드를 방문한다. 루트를 가장 마지막에 방문하기 때문에 하위 노드의 처리가 모두 끝난 뒤 상위 노드를 처리해야 하는 상황에 적합하다. 대표적인 예로 트리 삭제 연산이 있다. 부모 노드를 삭제하기 전에 자식 노드를 먼저 제거해야 메모리 오류를 방지할 수 있기 때문에 후위 순회가 자연스럽게 사용된다. 또한 수식 트리에서는 후위 순회 결과가 후위 표기식이 되며, 이는 계산기 구현이나 컴파일러 설계에서 중요한 역할을 한다. 후위 순회는 처음 접하면 직관적으로 이해하기 어렵지만, “나중에 처리한다”는 개념을 중심으로 접근하면 활용 목적이 명확해진다. 실제 개발 환경에서도 의존 관계가 있는 작업을 순차적으로 처리해야 할 때 후위 순회의 개념이 응용된다. 이런 점에서 후위 순회는 단순한 학습 개념을 넘어 실무 사고방식에도 영향을 준다.
전위, 중위, 후위 순회는 단순히 방문 순서만 다른 것이 아니라 각각 뚜렷한 목적과 활용 사례를 가진다. 트리 구조를 이해하고 문제에 맞는 순회 방식을 선택할 수 있다면 알고리즘 문제 해결 능력은 물론 전반적인 자료구조 이해도 역시 크게 향상된다. 세 가지 순회 원리를 비교하며 반복 학습하는 것이 가장 효과적인 학습 방법이다.