시간 복잡도와 공간 복잡도는 알고리즘의 성능을 분석하고 평가하는 데 있어 가장 기본이자 핵심적인 기준이다. 동일한 결과를 출력하는 프로그램이라 하더라도, 어떤 알고리즘을 사용하느냐에 따라 실행 속도와 메모리 사용량은 큰 차이를 보인다. 특히 2026년 기준으로 코딩 테스트, 실무 개발, 대규모 데이터 처리 환경에서는 복잡도 개념을 정확히 이해하지 못하면 성능 문제를 해결하기 어렵다. 이 글에서는 시간 복잡도와 공간 복잡도의 정의부터 빅오 표기법, 실제 선택 기준까지 초보자 눈높이에 맞춰 체계적으로 설명한다.
시간 복잡도란? 실행 속도를 판단하는 기준
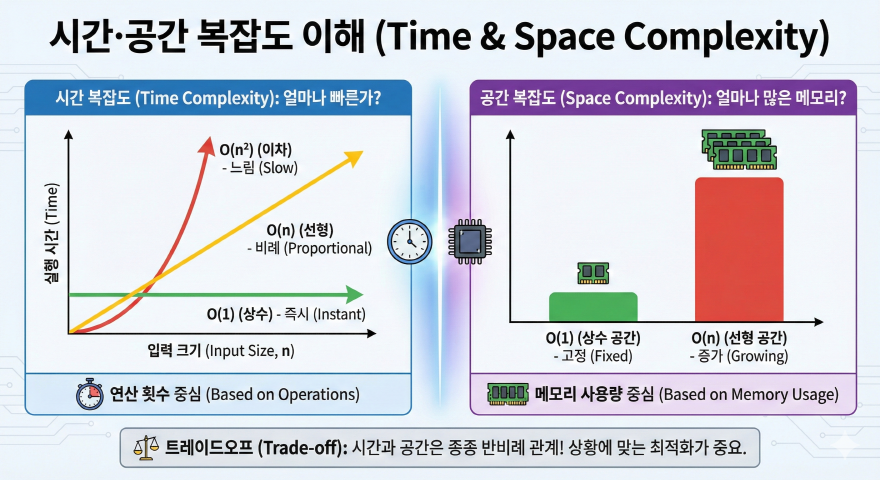
시간 복잡도는 알고리즘이 입력 데이터의 크기에 따라 얼마나 많은 연산을 수행하는지를 나타내는 척도다. 여기서 중요한 점은 실제 실행 시간이 아니라, 입력 크기가 증가했을 때 연산 횟수가 어떤 비율로 증가하는지를 본다는 것이다. 이를 통해 하드웨어 성능이나 실행 환경과 무관하게 알고리즘 자체의 효율을 비교할 수 있다.
시간 복잡도를 표현할 때 가장 널리 사용되는 방식이 빅오(Big-O) 표기법이다. 빅오는 알고리즘의 최악의 경우를 기준으로 성능을 단순화해 표현한다. 예를 들어 O(1)은 입력 크기와 관계없이 항상 일정한 연산만 수행하는 경우이며, O(n)은 입력 크기에 비례해 연산 횟수가 증가하는 구조다. 반복문이 두 번 중첩되면 O(n²), 세 번 중첩되면 O(n³)처럼 복잡도는 급격히 커진다.
초보자들이 흔히 착각하는 부분은 코드가 짧으면 빠를 것이라는 생각이다. 하지만 실제로는 반복문의 구조, 조건 분기, 자료 접근 방식이 시간 복잡도에 훨씬 큰 영향을 미친다. 따라서 알고리즘을 작성할 때는 입력 값이 매우 커졌을 때도 효율적으로 동작할 수 있는지를 기준으로 판단하는 습관이 필요하다.
공간 복잡도란? 메모리 사용량의 척도
공간 복잡도는 알고리즘이 실행되는 동안 얼마나 많은 메모리를 사용하는지를 나타내는 지표다. 이는 단순히 입력 데이터를 저장하는 공간만을 의미하지 않는다. 알고리즘 내부에서 사용하는 변수, 배열, 객체, 그리고 재귀 호출 시 사용되는 호출 스택까지 모두 공간 복잡도에 포함된다.
공간 복잡도 역시 빅오 표기법으로 표현한다. 예를 들어 입력 크기 n에 비례하는 배열을 새로 생성한다면 공간 복잡도는 O(n)이 된다. 반대로 입력 크기와 무관하게 일정한 개수의 변수만 사용한다면 O(1)의 공간 복잡도를 가진다. 특히 재귀 알고리즘은 코드가 간결해 보이지만 호출 깊이에 따라 스택 메모리를 많이 사용할 수 있으므로 공간 복잡도를 반드시 함께 고려해야 한다.
현대 개발 환경에서는 메모리가 과거보다 풍부해졌지만, 모바일 앱, 임베디드 시스템, 대규모 서버 환경에서는 여전히 메모리 효율이 중요한 요소다. 따라서 공간 복잡도를 무시한 설계는 성능 저하나 시스템 장애로 이어질 수 있다.
시간 복잡도와 공간 복잡도의 관계와 선택 기준
시간 복잡도와 공간 복잡도는 서로 독립적인 개념이지만, 실제 문제 해결 과정에서는 트레이드오프 관계에 놓이는 경우가 많다. 실행 속도를 빠르게 만들기 위해 메모리를 더 사용하는 경우가 대표적이다. 캐싱이나 메모이제이션 기법은 이전 계산 결과를 저장해 반복 연산을 줄이는 방식으로, 공간을 희생해 시간을 절약하는 전략이다.
코딩 테스트 환경에서는 일반적으로 시간 복잡도가 가장 중요한 평가 요소가 된다. 입력 크기가 큰 문제에서 시간 초과는 곧 오답으로 처리되기 때문이다. 반면 실무 개발에서는 메모리 비용, 서버 자원, 유지 보수성까지 함께 고려해야 한다. 이 때문에 무조건 가장 빠른 알고리즘이 아니라, 상황에 가장 적합한 알고리즘을 선택하는 판단력이 중요해진다.
초보자는 먼저 시간 복잡도를 중심으로 알고리즘 효율을 판단하는 연습을 하고, 이후 공간 복잡도까지 함께 고려하는 단계로 학습을 확장하는 것이 효과적이다.
시간 복잡도는 알고리즘의 실행 효율을 판단하는 기준이며, 공간 복잡도는 메모리 사용 효율을 평가하는 지표다. 이 두 가지 개념을 정확히 이해하면 단순히 동작하는 코드를 넘어, 효율적이고 안정적인 프로그램을 설계할 수 있다. 알고리즘 학습 초기 단계에서 복잡도 개념을 확실히 다져두는 것은 코딩 테스트와 실무 개발 모두에서 큰 경쟁력이 된다.