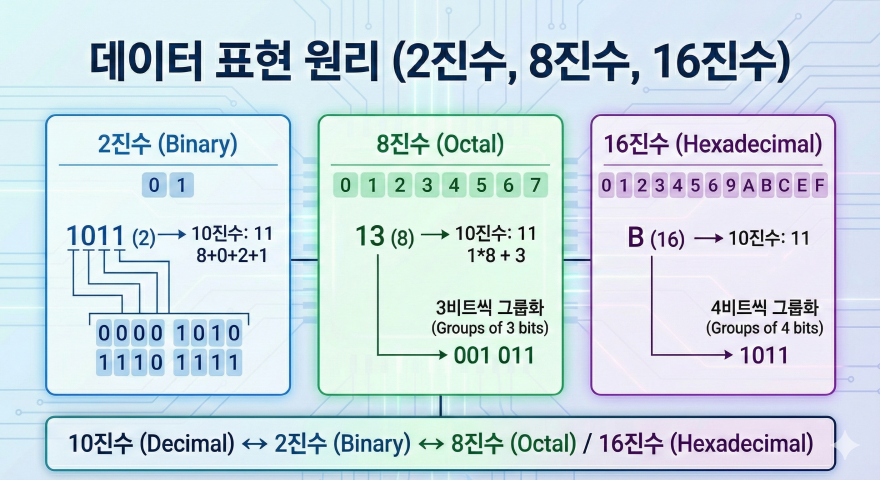
컴퓨터와 디지털 기기는 우리가 사용하는 10진수가 아닌 다른 진법을 기반으로 데이터를 처리한다. 특히 2진수, 8진수, 16진수는 컴퓨터 구조와 프로그래밍의 핵심 개념으로 서로 밀접한 관계를 가진다. 이 글에서는 각 진수의 데이터 표현 원리와 상호 변환 방법을 체계적으로 정리해, 초보자도 쉽게 이해할 수 있도록 설명한다.
2진수의 데이터 표현 원리
2진수는 컴퓨터가 데이터를 처리하는 가장 기본적인 진법이다. 전자 회로에서 전류의 흐름은 켜짐과 꺼짐, 즉 0과 1의 상태로만 구분할 수 있기 때문에 컴퓨터는 자연스럽게 2진수를 사용한다. 모든 데이터는 결국 비트(bit) 단위의 0과 1 조합으로 저장되며, 이 비트들이 모여 바이트(byte), 워드(word) 등의 단위를 이룬다. 예를 들어 문자, 숫자, 이미지, 영상까지 모두 2진수로 변환되어 저장되고 처리된다.
2진수는 자리값 개념이 매우 명확하다. 오른쪽부터 2의 0제곱, 2의 1제곱, 2의 2제곱 순으로 증가하며 각 자리에 0 또는 1이 들어간다. 예를 들어 1011이라는 2진수는 1×2³ + 0×2² + 1×2¹ + 1×2⁰으로 계산되어 10진수 11이 된다. 이러한 방식은 연산 과정이 단순하고 오류가 적어 하드웨어 구현에 최적화되어 있다.
하지만 2진수는 사람이 읽고 이해하기에는 불편하다. 숫자가 길어질수록 가독성이 급격히 떨어지기 때문에, 이를 보완하기 위해 8진수와 16진수가 함께 사용된다. 이 진수들은 2진수와 구조적으로 밀접한 관계를 가지며, 변환이 매우 간단하다는 장점이 있다.
8진수의 데이터 표현 원리
8진수는 0부터 7까지의 숫자를 사용하는 진법으로, 2진수를 사람이 읽기 쉽게 표현하기 위해 만들어졌다. 8진수의 가장 큰 특징은 2진수 세 자리를 하나의 숫자로 묶을 수 있다는 점이다. 이는 8이 2의 세 제곱이라는 사실에서 비롯된다. 예를 들어 2진수 000부터 111까지는 각각 8진수 0부터 7에 정확히 대응된다.
이러한 구조 덕분에 2진수를 8진수로 변환할 때는 오른쪽부터 세 자리씩 끊어 각 묶음을 10진수로 바꾸기만 하면 된다. 예를 들어 2진수 110101는 110과 101로 나누어 각각 6과 5가 되어 8진수 65로 표현된다. 반대로 8진수를 2진수로 변환할 때도 각 자리를 세 자리 2진수로 바꾸면 되므로 계산 과정이 매우 단순하다.
과거에는 메모리 주소나 시스템 권한 표현 등에서 8진수가 자주 사용되었다. 특히 유닉스 계열 운영체제에서 파일 권한을 표현할 때 8진수를 사용하는 전통은 지금도 이어지고 있다. 다만 현대 개발 환경에서는 16진수에 비해 사용 빈도가 줄어든 편이다.
16진수의 데이터 표현 원리
16진수는 0부터 9까지의 숫자와 A부터 F까지의 문자를 사용하여 총 16개의 값을 표현하는 진법이다. 2진수 네 자리를 하나로 묶을 수 있기 때문에, 매우 긴 2진수를 짧고 직관적으로 표현할 수 있다. 예를 들어 2진수 11111111은 16진수로 FF가 되어 훨씬 읽기 쉬워진다.
16진수는 메모리 주소, 색상 코드, 기계어 표현 등 컴퓨터 과학 전반에서 폭넓게 사용된다. 특히 웹 개발에서 색상을 표현할 때 사용하는 #FFFFFF 같은 코드도 16진수 기반이다. 각 두 자리씩이 빨강, 초록, 파랑 값을 나타내며, 내부적으로는 모두 2진수로 변환되어 처리된다.
2진수에서 16진수로의 변환은 네 자리씩 끊어 계산하면 되므로 매우 효율적이다. 예를 들어 2진수 10101111은 1010과 1111로 나누어 각각 A와 F가 되어 16진수 AF로 변환된다. 이러한 간편한 변환 구조 덕분에 개발자와 시스템 엔지니어에게 가장 널리 사용되는 진법이 되었다.
2진수, 8진수, 16진수는 각각 독립적인 진법이 아니라 데이터 표현이라는 하나의 목적 아래 긴밀하게 연결된 체계다. 2진수는 컴퓨터의 근본적인 언어이고, 8진수와 16진수는 이를 사람이 이해하기 쉽게 만든 표현 방식이다. 이 관계와 변환 원리를 이해하면 컴퓨터 구조, 프로그래밍, 시스템 전반에 대한 이해도가 크게 향상된다. 기초 개념일수록 정확히 익혀두는 것이 중요하다.